Answers
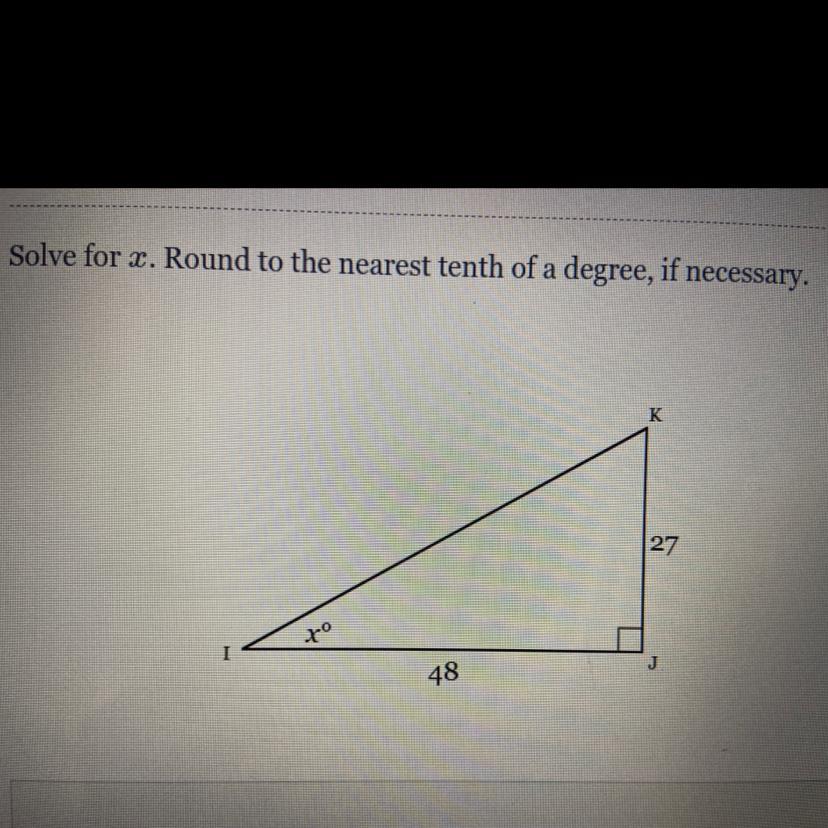
The value of angle x in the right triangle KJI is approximately 63.4 degrees.
What is trigonometric ratios ?
Trigonometric ratios are mathematical functions that relate the angles of a right triangle to the lengths of its sides. The three primary trigonometric ratios are sine, cosine, and tangent, which are abbreviated as sin, cos, and tan, respectively.
These ratios are defined as follows:
Sine (sin) of an angle is the ratio of the length of the side opposite to the angle to the length of the hypotenuse.
Cosine (cos) of an angle is the ratio of the length of the adjacent side to the angle to the length of the hypotenuse.
Tangent (tan) of an angle is the ratio of the length of the side opposite to the angle to the length of the adjacent side.
Finding the value of x :
We can use the trigonometric ratios to find the value of angle x in the right triangle KJI.
First, we can use the Pythagorean theorem to find the length of the hypotenuse KI:
[tex]KI^2 = KJ^2 + JI^2[/tex]
[tex]KI^2 = 27^2 + 48^2[/tex]
[tex]KI^2 = 729 + 2304[/tex]
[tex]KI^2 = 3033[/tex]
[tex]KI =\sqrt{3033}[/tex]
Next, we can use the sine function to find the value of angle I:
[tex]sin(I) = JI / KI[/tex]
[tex]sin(I) = 48 / \sqrt{3033}[/tex]
[tex]I = sin^-1(48 / \sqrt{3033})[/tex]
[tex]I = 63.4[/tex] degrees
Therefore, the value of angle x in the right triangle KJI is approximately 63.4 degrees.
To know more about angle visit :
brainly.com/question/28451077
#SPJ1
Related Questions
What is the volume of this cylinder? Use n 3.14 and round your answer to the nearest hundredth.
Answers
Answer:
9231.60 cubic inches
Step-by-step explanation:
V = [tex]\pi r^{2} h[/tex]
V = [tex]\pi (14)^{2} (15)[/tex]
V = 9231.60 cubic inches
How to turn 0. 1212121212 into a simplified fraction
Answers
Answer:
4/33
Step-by-step explanation:
You want to write 0.1212...(repeating) as a simplified fraction.
Repeating decimalA repeating decimal beginning at the decimal point can be made into a fraction by expressing the repeating digits over an equal number of 9s.
Here, there are 2 repeating digits, so the basic fraction is ...
12/99
This can be reduced by removing a factor of 3 from numerator and denominator:
[tex]0.\overline{12}=\dfrac{12}{99}=\boxed{\dfrac{4}{33}}[/tex]
__
Additional comment
Formally, you can multiply any repeating decimal by 10 to the power of the number of repeating digits, then subtract the original number. This gives the numerator of the fraction. The denominator is that power of 10 less 1.
0.1212... = (12.1212... - 0.1212...)/(10^2 -1) = 12/99
Doing this multiplication and subtraction also works for numbers where the repeating digits don't start at the decimal point. Finding a common factor with 99...9 may not be easy.
You can also approach this by writing the number as a continued fraction. The basic form is ...
[tex]x=a+\cfrac{1}{b+\cfrac{1}{c+\cdots}}[/tex]
where 'a' is the integer part of the original number, and b, c, and so on are the integer parts of the inverse of the remaining fractional part. The attachment shows how this works for the fraction in the problem statement.
A calculator cannot actually represent a repeating decimal exactly, so error creeps in and may eventually become significant.
Can somebody help me with this?
Answers
Answer:
the distance between P and Q is ≈ 6.2 units
Step-by-step explanation:
calculate the distance d using the distance formula
d = [tex]\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }[/tex]
with (x₁, y₁ ) = P (1, 5 ) and (x₂, y₂ ) = Q (5.5, 9.25 )
d = [tex]\sqrt{(5.5-1)^2+(9.25-5)^2}[/tex]
= [tex]\sqrt{(4.5)^2+(4.25)^2}[/tex]
= [tex]\sqrt{20.25+18.0625}[/tex]
= [tex]\sqrt{38.3125}[/tex]
≈ 6.2 ( to the nearest tenth )
bacteria such as v. cholerae are known to follow an exponential growth curve rate, and will double their number every 15 minutes. fortunately, anti-bacterial hand wash can kill 99.9% of bacteria on a surface. if a colony of 500 v. cholerae cells are left alone for 2 hours, then anti-bacterial handwash is applied thoroughly, how many bacterial cells are left?
Answers
After using the antibacterial hand wash, there will be a remaining count of 203 bacterial cells.
The initial colony has 500 bacterial cells. We need to find the number of bacterial cells that will be left after 2 hours if an antibacterial hand wash is applied thoroughly. The antibacterial hand wash can kill 99.9% of the bacteria on a surface.
The doubling time of bacteria is given as 15 minutes. This means that every 15 minutes, the bacterial population doubles, which gives us an exponential growth rate. Therefore, the growth rate is given as follows:k = ln2 / Td where k is the growth rate, and Td is the doubling time.
Substituting the values we get:k = ln2 / 15min = 0.0462 min⁻¹We can find the number of bacteria present after a time t if the initial number of bacteria is N0 and the population growth rate is k using the following equation: Nt = N0 * e^(kt)where Nt is the number of bacteria after time t.As we know, the bacterial colony has 500 cells initially.
We can find the number of bacterial cells after 2 hours, which is 120 minutes, using the following equation: Nt = 500 * e^(0.0462 * 120min) = 202,599 bacteria. However, after applying an antibacterial hand wash, 99.9% of the bacteria will be killed.
This means that only 0.1% of the bacterial population will remain. We can find the number of bacteria that will be left using the following formula:N_final = N_initial * (1 - %killed)N_final = 202,599 * (1 - 0.999) = 203 bacteria
Therefore, there will be 203 bacterial cells left after applying the antibacterial hand wash.
To know more about exponential growth rate refer here:
https://brainly.com/question/1596693#
#SPJ11
a collection of five positive integers has mean $4.4$, unique mode $3$ and median $4$. if an $8$ is added to the collection, what is the new median? express your answer as a decimal to the nearest tenth.
Answers
To begin, we know that the median of the original collection of five positive integers is 4, which means that the middle number is 4. We also know that the unique mode is 3, which means that there is only one number in the collection that occurs more frequently than any other number.
Let's call the five positive integers in the original collection a, b, c, d, and e.
Since the mean of the original collection is 4.4, we can set up the equation:
(a+b+c+d+e)/5 = 4.4
Multiplying both sides by 5 gives:
a+b+c+d+e = 22
We also know that the mode is 3, which means that one of the numbers in the collection must be 3. Let's assume that a = 3, then we have:
3+b+c+d+e = 22
b+c+d+e = 19
Since the median is 4 and 3 is the unique mode, we can conclude that b, c, d, and e must be either 4 or 5. However, since there is only one unique mode, we know that there is only one number in the collection that is equal to 3. Therefore, we can conclude that the collection of five positive integers must be: 3, 4, 4, 4, 5.
If we add 8 to this collection, the new collection becomes: 3, 4, 4, 4, 5, 8. The new collection has six numbers, so the median is now the average of the two middle numbers. Since the middle two numbers are 4 and 5, the median is (4+5)/2 = 4.5.
Therefore, the new median is 4.5, expressed as a decimal to the nearest tenth.
For more details about median click here:
https://brainly.com/question/28060453#
#SPJ11
Find the terms through degree 4 of the Maclaurin series of . Use multiplication and substitution as necessary.
[tex]f(x)=\frac{4sin(2x)}{1-x}[/tex]
Answers
The terms through degree 4 of the Maclaurin series of f(x) is [tex]8x+8x^{2} +(\frac{16}{3})x^{3}+(\frac{28}{3} ) x^{4}[/tex]
Describe Maclaurin Series?A Maclaurin series is a representation of a function as an infinite sum of terms involving its derivatives evaluated at a specific point, usually 0. It is a special case of a Taylor series, where the point of evaluation is 0.
The Maclaurin series is named after the Scottish mathematician Colin Maclaurin, who first used this method to study the properties of functions.
The general form of a Maclaurin series is:
[tex]f(x)=f(0)+f'(0)x+f''(0)x^{\frac{2}{2} } !+f'''(0)x^{\frac{3}{3} } !+....[/tex]
where f(0), f'(0), f''(0), f'''(0), etc. are the function and its derivatives evaluated at x = 0.
Maclaurin series can be used to approximate the value of a function at any point near 0, provided that the function has a sufficient number of derivatives at that point. They are commonly used in calculus, physics, and engineering to solve problems involving complex functions.
To find the Maclaurin series for [tex]f(x)=\frac{4sin2x}{1-x}[/tex], we can start by using the Maclaurin series for sin(2x) and for [tex](1-x)^{-1}[/tex]:
[tex]sin(2x)= 2x-2x^{\frac{3}{3} } !+2x^{\frac{5}{5} } !-...........\\(1-x)^{-1} =1+x+x^{2} +x^{3}+x^{4} +.....[/tex]
We can substitute these series into f(x) and multiply them together, then collect like terms:
[tex]f(x)=\frac{4sinx}{1-x} \\=4(2x-2x^{\frac{3}{3} }!+2x^{\frac{5}{5} }! -......)(1+x+x^{2} +x^{3}+x^{4+}.....)\\ =(8x+8x^{2} +8x^{3}+8x^{4}+....) -(8x^{\frac{3}{3} }!+8x^{\frac{5}{5} } ! +....)+(16x^{\frac{5}{5} }! +....)[/tex]
We can simplify this expression to get the first few terms of the Maclaurin series:
[tex]f(x)= 8x+8x^{2} +8x^{3}-8x^{4}-8x^{\frac{3}3} }-8x^{\frac{5}{30} }+ 16x^{\frac{5}{120} }+......=8x+ 8x^{2}+(\frac{16}{3}) x^{3}+(\frac{28}{3} ) x^{4}-(\frac{2}{15} ) x^{5} +............[/tex]
Therefore, the terms through degree 4 of the Maclaurin series of f(x) are:
[tex]8x+8x^{2} +(\frac{16}{3})x^{3}+(\frac{28}{3} ) x^{4}[/tex]
To know more about expression visit:
https://brainly.com/question/24188694
#SPJ1
Triangle LMN is drawn with vertices at L(−3, −2), M(1, −4), N(−3, −4). Determine the image vertices of L′M′N′ if the preimage is rotated 90° clockwise.
L′(−3, −2), M′(1, −4), N′(−3, −4)
L′(−2, 3), M′(−4, −1), N′(−4, 3)
L′(3, 2), M′(−1, 4), N′(3, 4)
L′(2, 3), M′(4, −1), N′(4, 3)
QUICK HELP 30 POINTS
Answers
The image vertices of L′M′N′ are (-2, 3), (-4, -1), and (-4, 3).
What is preimage?
The set of all domain elements for a given function that map to a certain subset of the codomain; (formally) given a function X Y and a subset B Y, the set 1(B) = x X: x B.
Here, we have
Given: Triangle LMN is drawn with vertices at L(−3, −2), M(1, −4), N(−3, −4).
We have to determine the image vertices of L′M′N′ if the preimage is rotated 90° clockwise.
The rule for rotating a point (x, y) 90° clockwise is:
(x,y) ⇒ (y, -x)
The vertices of triangle LMN will be mapped to:
L(-3,-2) ⇒L' (-2, 3)
M(1,-4) ⇒ M'(-4, -1)
N(-3,-4) ⇒ N'(-4, 3)
Hence, the image vertices of L′M′N′ are (-2, 3), (-4, -1), and (-4, 3).
To learn more about the preimage from the given link
https://brainly.com/question/30895103
#SPJ1
what is 3x^4-73x^2-50 factored
Answers
Answer:
(3x - 10)(x - 5)
Step-by-step explanation:
That expression is equal to (3x^4 -73x^2 - 50). This factored expression can be written as (3x^2 -17x - 17) * (x+2.5) and can be factored using the FOIL method. (FOIL) - First, Outer, Inner, Last. This method ensures that you include all of the terms with the same variables. The FOIL method is very easy and helpful for factoring complex equations and is something that is good to be familiar with for future study if you are looking to delve deeper into math!
The expression (3x^4 - 73x^2 - 50) factored is an example of a quadratic equation and the expression can be factored into (3x - 10)(x - 5). I think this is a good exercise because it shows how quadratic equations can be factored and the process involved, so students can apply the principles learned to other situations and problems they may encounter later on. It's important to understand how to factor quadratics since they often show up in real-world situations such as physics or statistics, so it's a great thing to have these skills locked in.
What is 3(25+19) + 4(3)
Answers
The value of the expression given is 144
What is an expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given is an expression 3(25+19) + 4(3) we need to simplify,
Using PEMDAS,
3(25+19) + 4(3)
= 75+57 + 12
= 132+12
= 144
Hence, the value of the expression given is 144
Learn more about expression, click;
https://brainly.com/question/14083225
#SPJ2
Ex. 1: Last year, the price of a lawnmower was $358.99. The same model sells
for $329.99 this year. What is the percent change in the price of the
over the 2 years? Round your answer to the nearest tenth.
lawnmower
Answers
The percent change in the price of the lawnmower over the 2 years is -8.1%.
Calculating the percentage changeTo find the percent change in the price of the lawnmower over the 2 years, we can use the formula:
percent change = (new value - old value) / old value * 100%
Plugging in the values given in the problem, we get:
percent change = (329.99 - 358.99) / 358.99 * 100%
percent change = -8.1%
Therefore, the percent change in the price of the lawnmower over the 2 years is -8.1%. Note that the negative sign indicates a decrease in price.
Read more about percentage change at
https://brainly.com/question/23885199
#SPJ1
Write a quadratic function to represent the relationship shown in the table.
Answers
The quadratic function that represents the relationship in the given table is y =[tex]-2x^2 + 8x + 4,[/tex] which was verified by substituting the x-values from the table into the equation.
The quadratic function that represents the relationship in the given table is y [tex]= -2x^2 + 8x + 4.[/tex]To verify this, we can substitute the x-values from the table into the equation and compare the resulting y-values.
When x = 0, we get y =[tex]-2(0)^2 + 8(0) + 4 = 4[/tex], which matches the table.
When x = 1, we get y =[tex]-2(1)^2 + 8(1) + 4 = 4,[/tex] which matches the table.
When x = 2, we get y =[tex]-2(2)^2 + 8(2) + 4 = 2,[/tex] which matches the table.
When x = 3, we get y =[tex]-2(3)^2 + 8(3) + 4 = 4,[/tex] which matches the table.
When x = 4, we get y = [tex]-2(4)^2 + 8(4) + 4 = 6,[/tex] which matches the table.
Therefore, the quadratic function y =[tex]-2x^2 + 8x + 4[/tex]accurately represents the relationship in the given table.
Learn more about quadratic here:
https://brainly.com/question/22364785
#SPJ1
Find the x- and y-intercepts of the function f(x) = log(2x + 1) − 1.
The x-intercept of the function f(x) = log(2x + 1) − 1 is
. Its y-intercept is
Answers
The x-intercept is (4.5, 0) and y-intercept is (0, -1) for the given function.
What are intercepts ?
Intercepts are the points at which a curve intersects with the x-axis and y-axis on a coordinate plane. The x-intercept is the point where the curve intersects with the x-axis, and its y-coordinate is zero. The y-intercept is the point where the curve intersects with the y-axis, and its x-coordinate is zero. The intercepts provide useful information about the behavior and properties of a curve, such as its roots and symmetry.
According to the question:
To find the x-intercept, we need to set y = 0 and solve for x:
[tex]0 = log(2x + 1) - 11 = log(2x + 1)10 = 2x + 19 = 2xx = 4.5[/tex]
Therefore, the x-intercept is (4.5, 0).
To find the y-intercept, we need to set x = 0 and evaluate the function:
[tex]f(0) = log(2(0) + 1) - 1[/tex]
= 0 - 1[tex]= log(1) - 1[/tex]
= -1
Therefore, the y-intercept is (0, -1).
To know more about intercepts visit:
brainly.com/question/14180189
#SPJ1
I dont know what to do help please :(
Answers
Answer:
18x +48 +32 +12x30x +8010(3x +8)Step-by-step explanation:
You want three additional equivalent expressions to 6(3x +8) +32 +12x, one of which is the expression in simplest form.
Equivalent expressionsAny expression you write along the path to simplifying the given expression will be an equivalent. Here's one way to get three different expressions:
6(3x +8) +32 +12x . . . . . . given
18x +48 +32 +12x . . . . . . eliminate parentheses
30x +48 +32 . . . . . . . . . . combine x terms
30x +80 . . . . . . . . . . . . . . combine constants (2 terms)
We can write another equivalent by factoring out a common factor:
10(3x +8)
factorise (a-b+c)²-(b-c+a)²
Answers
Answer: (a-b+c)²-(b-c+a)²
=((a-b+c)) - ((b-c+a)) ((a-b+c)) - ((b-c+a))
= (a-b+c-b+c-a) ( a-b+c+b-c+a)
= (-2b + 2c ) (2a)
= (2( -2b/2+2c/2)) (2a)
=(2(-b+c)) (2a)
=2(-b+c) (2a)
Draw a figure composed of three different rectangle that has a perimeter of 140 yards use measurements in yards in feet to label this side of your figures.
Answers
To create a figure of three rectangles with a perimeter of 140 yards, you can stack them on top of each other to make a plus sign, and label each side as 11 and 2/3 yards or 11 yards (by subtracting the fractions).
What is rectangle?A rectangle is a four-sided geometric shape that has four right angles (90 degree angles) and opposite sides that are parallel and of equal length. The length of a rectangle is its longer side, while the width is its shorter side.
According to given information:If we draw three rectangles stacked on top of each other like a plus sign, we can divide the perimeter of 140 yards by the number of sides, which is 12. This gives us a length of 11 and 2/3 yards per side.
To use only integers, we can subtract the fractions from each side to another, which gives us a length of 11 yards per side. We can then label each side of the figure with a length of 11 yards.
In the figure, we have three rectangles of equal size, with a length of 11 yards and a width of 35 yards. We can convert the measurements to feet by multiplying by 3, which gives us a length of 33 feet and a width of 105 feet.
Alternatively, if we wanted to use only whole numbers, we could increase the size of each rectangle slightly, so that the total perimeter is a multiple of 12. For example, we could make each rectangle 11.6667 yards by 35 yards, which gives us a total perimeter of 140.0008 yards. We can then divide this by 12 to get a length of 11 and 2/3 yards per side, and label each side with a length of 11 yards.
To know more about rectangle visit:
https://brainly.com/question/2607596
#SPJ9
Question A store gives away gift bags during a sale. Of these gift bags, 50% are green, 20% are yellow, and 30% are blue. The average number of items in each green bag is 8. The average number of items in each yellow bag is 5. The average number of items in each blue bag is 8. What is the average number of items in all the gift bags? Enter your answer as a decimal in the box.
Answers
The average number of items in all the gift bags is 7.4.
What is average?Average, also known as mean, is a numerical value that represents the central or typical value in a set of numbers. It is calculated by adding up all the numbers in a set and dividing the sum by the total number of values in the set. The average is a useful tool for summarizing a large amount of data into a single value that can be easily understood and compared to other values.
In the given question,
We can use the weighted average formula to find the average number of items in all the gift bags:
Average number of items = (proportion of green bags x average items in green bags) + (proportion of yellow bags x average items in yellow bags) + (proportion of blue bags x average items in blue bags)
Proportion of green bags = 50% = 0.5
Proportion of yellow bags = 20% = 0.2
Proportion of blue bags = 30% = 0.3
Average items in green bags = 8
Average items in yellow bags = 5
Average items in blue bags = 8
Substituting the values into the formula, we get:
Average number of items = (0.5 x 8) + (0.2 x 5) + (0.3 x 8)
Average number of items = 4 + 1 + 2.4
Average number of items = 7.4
Therefore, the average number of items in all the gift bags is 7.4
To know more about average, visit:
https://brainly.com/question/24057012
#SPJ1
A rectangle is shown. The length of the rectangle is labeled 5 inches. The width of the rectangle is labeled 8 inches.
A photographer wants to use a scale factor of 2.5 to enlarge a picture. What will the area of the picture be after it is enlarged? (5 points)
40 in2
250 in2
100 in2
81.9 in2
Answers
= 6.25
So true required area = 8*5*6.25
= 250
Two polygons are similar. The perimeter of the larger polygon is 120 yards and the ratio of the corresponding side lengths is $\frac{1}{6}$. Find the perimeter of the other polygon
Answers
The perimeter of the smaller polygon is 20 yards.
Two polygons are similar.
The perimeter of the larger polygon is 120 yards and the ratio of the corresponding side lengths is 1/6.
Find the perimeter of the other polygon.
In similar polygons, the ratio of the corresponding side lengths is equal to the ratio of their perimeters.
Since the larger polygon has a perimeter of 120 yards and the ratio of the corresponding side lengths is 1/6,
the smaller polygon must have a perimeter that is 1/6 of the larger polygon's perimeter.
That is, Perimeter of smaller polygon = [tex]\frac {1}{6}[/tex]
The perimeter of larger polygon= [tex]\frac{1}{6} \times120\][/tex]
Multiplying 1/6 by 120 yields
[tex]\frac{120}{6}[/tex] =20
So the perimeter of the smaller polygon is 20 yards.
For similar question on perimeter.
https://brainly.com/question/19819849
#SPJ11
PLS SHOW HIW U DID IT PLSSSEE....and thank you.
Answers
Answer:
I think it is 399.
Step-by-step explanation:
if AD = 85 and BC =31 find the value of x
Answers
Thus, the value of x found by Chord Arcs Theorem for the given Arc AD and arc CD is found as: x = 11.
Explain about the Chord Arcs Theorem?The chords of such a circle are covered by a number of theorems. The chord arcs theorem is one such example. The intercepted arcs with congruent chords also were congruent according to this theorem.
Now,
chord AB = chord DC
Thus,
m AB = m DC = 13x - 21
For the complete circle: angle = 360.
AB + DC + AD + BC = 360
(13x - 21) + (13x - 21) + 85 + 31 = 360
(36x - 42) + 116 = 360
26x - 42 = 244
26x = 244 + 42
x = 286/26
x = 11
Thus, the value of x found by Chord Arcs Theorem for the given Arc AD and arc CD is found as: x = 11.
Know more about the Chord Arcs Theorem
https://brainly.com/question/17004780
#SPJ1
Complete question:
if m AD = 85 and m BC =31 find the value of x.
The diagram is attached.
How many Hamiltonian circuits exists in a complete graph with 11 vertices?
10!
12!
11!
9!
Answers
An [tex]11[/tex]-vertex full graph has around [tex]19,958,931,200[/tex] Hamiltonian circuits in a complete graph.
Describe the Hamiltonian circuit with an example.At one vertex, the Hamiltonian route begins, and at another, it finishes. Yet, when following a Hamiltonian route, every vertex is encountered. At the same vertex, the Hamiltonian circuit begins and terminates. For instance, if a Hamiltonian circuit's path began at vertex 1, the loop will also conclude at that vertex.
The Hamiltonian circuit: what is it?Single circuit is the sole trip a Hamiltonian circuit makes to each vertex. It must begin and terminate at same vertex since it is a circuit. A Hamiltonian route does not start and end in a single location, but it does visit each vertex just once with no repetitions.
We have to divide by [tex]2(n-2)[/tex]
[tex]11!/(2(11-2)!) = 11!/2,520[/tex] Hamiltonian circuits we get:
[tex]11!/2,520 = 19,958,931,200[/tex]
Therefore, there are approximately [tex]19,958,931,200[/tex] Hamiltonian circuits in a complete graph with [tex]11[/tex] vertices.
To know more about Hamiltonian circuits visit:
https://brainly.com/question/24103350
#SPJ1
divide the circumference of a pumpkin by its diameter and what do you get?
Answers
Dividing the circumference of a pumpkin by its diameter gives a value approximately equal to pi (π)
When you divide the circumference of a pumpkin by its diameter, you get a value that is approximately equal to the mathematical constant pi (π), which is approximately 3.14159.
This is because pi represents the ratio of the circumference of a circle to its diameter, and a pumpkin is roughly spherical in shape. So, no matter how big or small the pumpkin is, if you measure its circumference and diameter and divide them, the result will be very close to pi.
Mathematically, this can be represented by the formula
pi ≈ circumference / diameter
Learn more about Pi here
brainly.com/question/16277677
#SPJ4
if y varies directly as x, and y=7 when x=3, find when x=7
Answers
Direct variation means the ratio of y to x is constant.
y1/x1 = y2/x2 ⇒
y2 = (x2/x1) y1
Plug in
x1 = 3
y1 = 7
x2 = 7
and get y2.
the average athlete is able to begin activity 90 days after having a knee operation. the standard deviation is 15 days. fifty percent of athletes are able to participate within how many days? round to the nearest day.
Answers
On average, 50% of athletes are able to begin activity 90 days after a knee operation, with a standard deviation of 15 days.
This means that the median time for 50% of athletes to be able to participate is 75 days, rounded to the nearest day.
The average time for an athlete to begin activity after a knee operation is 90 days, and the standard deviation is 15 days.
Standard deviation is a measure of how spread out the data points are in a data set; a larger standard deviation means that the data points are more spread out.
In this case, 50% of athletes can begin activity within 75 days, which is the median. By rounding to the nearest day, this would be 75 days. Therefore, 50% of athletes are able to participate within 75 days, rounded to the nearest day.
To know more about standard deviation click on below link:
https://brainly.com/question/23907081#
#SPJ11
a sample of 313 people is surveyed. democrat republican or independent. what is the relative frequewasncy of respondents
Answers
The relative frequency of respondents for a sample of 313 people who identified as Democrat, Republican, or Independent can be calculated by dividing the number of respondents for each group by the total number of respondents (313).
For example, if 100 respondents identified as Democrat, the relative frequency of Democrats would be 100/313, or approximately 32%. If 125 respondents identified as Republican, the relative frequency of Republicans would be 125/313, or approximately 40%. If the remaining 88 respondents identified as Independent, the relative frequency of Independents would be 88/313, or approximately 28%.
Therefore, the relative frequency of respondents in the sample of 313 people would be 32% Democrat, 40% Republican, and 28% Independent.
Two thirds of a number X subtracted from four times the sum of y and 5
Answers
Answer: 4y - (2/3)x + 20
Step-by-step explanation:
Write out problem: 4(y+5) - (2/3)x
Expand: 4y + 20 - (2/3)x
Reorder: 4y - (2/3)x + 20
3 customers entered a store over the course of 12 minutes. Fill out a table of
equivalent ratios and plot the points on the coordinate axes provided.
Answers
Answer: the last box for minutes is 16
And the first box for customers is 1
Step-by-step explanation:
Answer:
See below.
Step-by-step explanation:
1st Box(First row)
We can set up a proportion to solve for the number of customers that would enter the store in 4 minutes:
3 customers is to 12 minutes as x customers is to 4 minutes
This can be written as:
3/12 = x/4
To solve for x, we can cross-multiply and simplify:
3/12 = x/4
3(4) = 12x
12 = 12x
x = 1
Therefore, we can expect 1 customer to enter the store in 4 minutes.
2nd Box(3rd Row)We can use the given ratios to find the time for 10 customers.
From the table, we can see that:
3 customers take 12 minutes.
1 customer takes 4 minutes (divide both sides of the ratio by 3).
So, 10 customers will take:
10 customers × 4 minutes per customer = 40 minutes.
Therefore, for 10 customers, the time is 40 minutes.
Which expression was factored completely using the GCF, if the original expression was
16x² + 8x?
4(4x²+2x)
4x(4x+2)
8(2x²+x)
8x(2x+1)
Answers
Answer:
It's D
Step-by-step explanation:
[tex]1. \: gcf = 8x \\ 2. \: 8x( \frac{16x {}^{2} }{8x} + \frac{8x}{8x} ) \\ 3. \: 8x(2x + 1)[/tex]
helppppp!! For #19-20, solve for x. Simplify all radicals.
Answers
19. x = 17
12. x = 8
(Rounded)
Explanation:
Help explain solve……
Answers
Answer:
About 92.1 °
Step-by-step explanation:
[tex]cos(U)=(58.8^{2} +38.4^{2} -71.4^{2} )/2(58.8)(38.4)\\[/tex]
[tex]cos(U)= (3457.44+1474.56-5097.96)/4515.84[/tex]
[tex]cos(U)= (-165.96)/4515.84[/tex]
[tex]cos(U)= -0.03675063775[/tex]
[tex]U= cos^{-1} (-0.03675)[/tex]
[tex]U=92.1[/tex]
Answer:
cosA=b^2+c^2-a^2/2xbxc
58.8^2+38.4^2-71.4^2/2x58.8x38.4=-461/12544
cos^-1 (because finding angle)
cos^1(-461/12544)=92.10613071